Revision as of 23:34, 20 December 2008

Conference article Steerable filters generated with the hypercomplex dual-tree wavelet transform

Introduction

Complex wavelets are superior to real-valued wavelets because they are nearly shift-invariant. Complex wavelets yield amplitude-phase information in a similar way as the Fourier transform does. In contrast to the Fourier transform, wavelets allow to analyse the signal locally and thus can be applied to signals with a non-stationary statistic (such as images of a natural scene). In the same way as a one-dimensional signal requires complex numbers to represent the local structure of the signal, two-dimensional signals require hypercomplex numbers. Kingsbury has developed the Dual-Tree Complex Wavelet Transform which allows to recursively compute complex wavelet transforms. Analogous to one-dimensional analysis requiring complex values, two-dimensional analysis requires 4-valued complex numbers (hypercomplex values). Bülow, Kingsbury, and others already have successfully used hypercomplex numbers for analysing two-dimensional signals.

Implementation

High- and low-frequency decomposition using the dual-tree complex wavelet transform. The approximate shift-invariance leads to reduced aliasing

HornetsEye now contains an implementation of the Dual-Tree Complex Wavelet Transform. The implementation makes use of Hilbert transform pairs of wavelet bases. The wavelet transform was implemented with HornetsEye's MultiArray class. Have a look at the hypercomplex wavelet example for more information.

Wavelet Editor

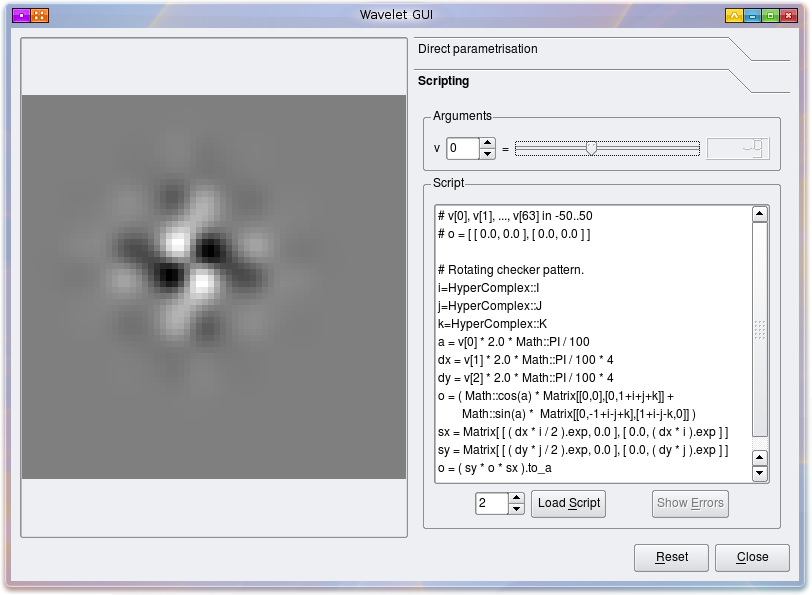
Wavelet editor

An editor for visualising linear combinations of wavelets was implemented. The code requires qt4-qtruby, and HornetsEye. The source code is part of the HornetsEye source package. You may need to compile the user interface design file using rbuic4 like this:

rbuic4 waveletEdit.ui > ui_waveletEdit.rb

You can view the source files in their current state at http://bazaar.launchpad.net/~wedesoft/hornetseye/trunk/files in the subdirectory samples/hypercomplex.

See Also

• HornetsEye
• Complex Wavelet Filters

External Links

• Ivan Selesnick's homepage
• Nick Kingsbury's homepage
  • N G Kingsbury: Complex wavelets for shift invariant analysis and filtering of signals, Journal of Applied and Computational Harmonic Analysis, vol 10, no 3, May 2001
  • J Fauqueur, N Kingsbury and R Anderson: Multiscale keypoint detection using the dual-tree complex wavelet transform, Proc. IEEE Conference on Image Processing, Atlanta, GA, 8-11 Oct 2006
• Thomas Bülow: Hypercomplex Spectral Signal Representations for Image Processing and Analysis, PhD thesis, 1999
• J. Wedekind, B. Amavasai, K. Dutton: Steerable Filters Generated With The Hypercomplex Dual-Tree Wavelet Transform, ICSPC07 proceedings (also see foils (PDF)) (I think there's a bug in the paper. I need to use <math>H_1(z)=(-z)^{-M}\,H_0(z^{-1})</math> (see Selesnicks paper) where <math>M</math> is odd. Maybe this explains the trouble I have with choosing the sampling offsets at the moment)
• Hypercomplex wavelet example
• Related work
  • Clyde Davenport's page on commutative hypercomplex mathematics
  • K. Krajsek, R. Mester: A Unified theory For Steerable And Quadrature Filters, International Conferences VISAPP and GRAPP 2006