Gradient Based Motion Estimation
m |
|||
| Line 1: | Line 1: | ||
[[Image:shift.jpg|thumb|200px|right|Detecting sub-pixel shifts]] | [[Image:shift.jpg|thumb|200px|right|Detecting sub-pixel shifts]] | ||
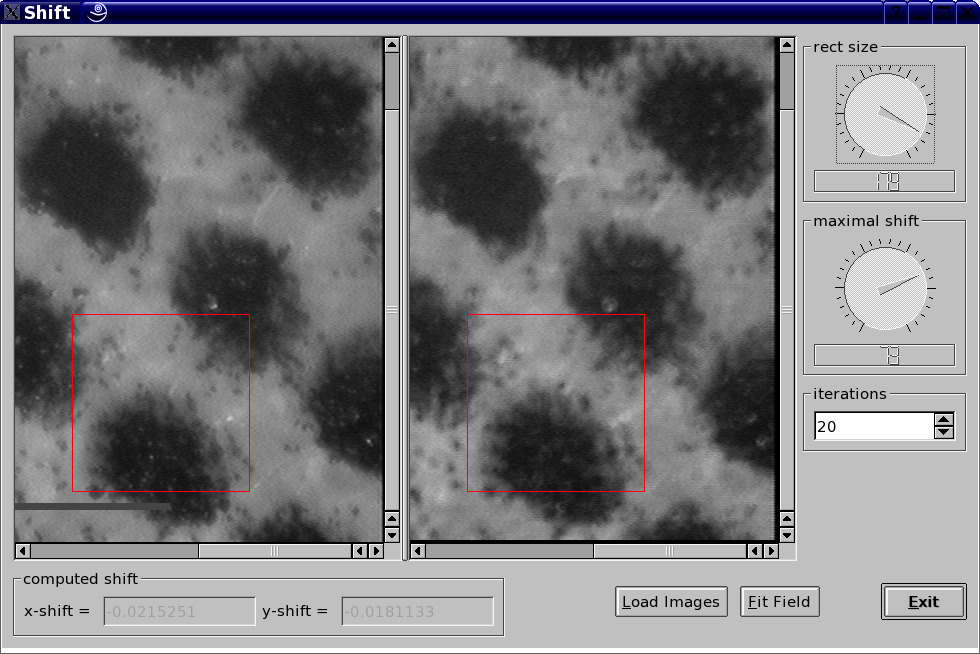
Using gradient based motion estimation is good at detecting sub-pixel shifts. During an investigation on depth of defocus, this software was developed for compensating the misalignment of a focus-drive. | Using gradient based motion estimation is good at detecting sub-pixel shifts. During an investigation on depth of defocus, this software was developed for compensating the misalignment of a focus-drive. | ||
| + | |||
| + | The local gradient <math>\cfrac{\delta g}{\delta\vec{x}}</math> of the gray values and the gradient in time <math>\cfrac{\delta g}{\delta t}</math> are related to each other in the first order: | ||
| + | |||
| + | <math>\Big(\cfrac{\delta g}{\delta x_1}(\vec{x},t)\ \cfrac{\delta g}{\delta x_2}(\vec{x},t)\Big)^\top\cdot\vec{v}(\vec{x},t)\approx-\cfrac{\delta g}{\delta t}(\vec{x},t)</math> where <math>g\in\mathbb{R}^2\times\mathbb{R}\mapsto\mathbb{R}</math> is a video and <math>\vec{v}\in\mathbb{R}^2\mapsto\mathbb{R}^2</math> a motion vector field. | ||
| + | |||
| + | Using the model <math>\vec{v}\big(\begin{pmatrix}x_1\\x_2\end{pmatrix}\big)=\begin{pmatrix}a_1+b_1\,x_1\\a_2+b_2\,x_2\end{pmatrix}</math> this becomes a least square problem: | ||
| + | <math>\begin{pmatrix} | ||
| + | \cfrac{\delta g}{\delta x_1}(\vec{p_1}) & p_{1,1}\,\cfrac{\delta g}{\delta x_1}(\vec{p_1}) & | ||
| + | \cfrac{\delta g}{\delta x_2}(\vec{p_1}) & p_{1,2}\,\cfrac{\delta g}{\delta x_2}(\vec{p_1}) \\ | ||
| + | \vdots & \vdots & \vdots & \vdots\\ | ||
| + | \cfrac{\delta g}{\delta x_1}(\vec{p_n}) & p_{n,1}\,\cfrac{\delta g}{\delta x_1}(\vec{p_n}) & | ||
| + | \cfrac{\delta g}{\delta x_2}(\vec{p_n}) & p_{n,2}\,\cfrac{\delta g}{\delta x_2}(\vec{p_n}) \\ | ||
| + | \end{pmatrix} | ||
| + | \begin{pmatrix} | ||
| + | a_1\\b_1\\a_2\\b_2 | ||
| + | \end{pmatrix}= | ||
| + | \begin{pmatrix} | ||
| + | -\cfrac{\delta g}{\delta t}(\vec{p_1})\\\vdots\\ | ||
| + | -\cfrac{\delta g}{\delta t}(\vec{p_n}) | ||
| + | \end{pmatrix} | ||
| + | +\vec{\epsilon} | ||
| + | </math> where <math>a_1</math>, <math>a_2</math> are denoting the shift and <math>b_1</math>, <math>b_2</math> are denoting the scale between the two images. | ||
| + | |||
| + | The result can be improved by applying the least square algorithm iteratively to the compensated images. | ||
Revision as of 11:01, 2 October 2005
Using gradient based motion estimation is good at detecting sub-pixel shifts. During an investigation on depth of defocus, this software was developed for compensating the misalignment of a focus-drive.
The local gradient <math>\cfrac{\delta g}{\delta\vec{x}}</math> of the gray values and the gradient in time <math>\cfrac{\delta g}{\delta t}</math> are related to each other in the first order:
<math>\Big(\cfrac{\delta g}{\delta x_1}(\vec{x},t)\ \cfrac{\delta g}{\delta x_2}(\vec{x},t)\Big)^\top\cdot\vec{v}(\vec{x},t)\approx-\cfrac{\delta g}{\delta t}(\vec{x},t)</math> where <math>g\in\mathbb{R}^2\times\mathbb{R}\mapsto\mathbb{R}</math> is a video and <math>\vec{v}\in\mathbb{R}^2\mapsto\mathbb{R}^2</math> a motion vector field.
Using the model <math>\vec{v}\big(\begin{pmatrix}x_1\\x_2\end{pmatrix}\big)=\begin{pmatrix}a_1+b_1\,x_1\\a_2+b_2\,x_2\end{pmatrix}</math> this becomes a least square problem: <math>\begin{pmatrix} \cfrac{\delta g}{\delta x_1}(\vec{p_1}) & p_{1,1}\,\cfrac{\delta g}{\delta x_1}(\vec{p_1}) & \cfrac{\delta g}{\delta x_2}(\vec{p_1}) & p_{1,2}\,\cfrac{\delta g}{\delta x_2}(\vec{p_1}) \\ \vdots & \vdots & \vdots & \vdots\\ \cfrac{\delta g}{\delta x_1}(\vec{p_n}) & p_{n,1}\,\cfrac{\delta g}{\delta x_1}(\vec{p_n}) & \cfrac{\delta g}{\delta x_2}(\vec{p_n}) & p_{n,2}\,\cfrac{\delta g}{\delta x_2}(\vec{p_n}) \\ \end{pmatrix} \begin{pmatrix} a_1\\b_1\\a_2\\b_2 \end{pmatrix}= \begin{pmatrix} -\cfrac{\delta g}{\delta t}(\vec{p_1})\\\vdots\\ -\cfrac{\delta g}{\delta t}(\vec{p_n}) \end{pmatrix} +\vec{\epsilon} </math> where <math>a_1</math>, <math>a_2</math> are denoting the shift and <math>b_1</math>, <math>b_2</math> are denoting the scale between the two images.
The result can be improved by applying the least square algorithm iteratively to the compensated images.