Mimas Camera Calibration
m |
m (→External Links) |
||
| (17 intermediate revisions by 3 users not shown) | |||
| Line 1: | Line 1: | ||
| − | [[Image: | + | {|align="right" |
| + | |- | ||
| + | |[[Image:Reconstruction_Platform.jpg|thumb|200px|Prototype low-cost platform for 3D reconstruction of objects using laser-triangulation ([http://vision.eng.shu.ac.uk/jan/reconstruction%20platform.avi 10 MByte video])]] | ||
| + | |- | ||
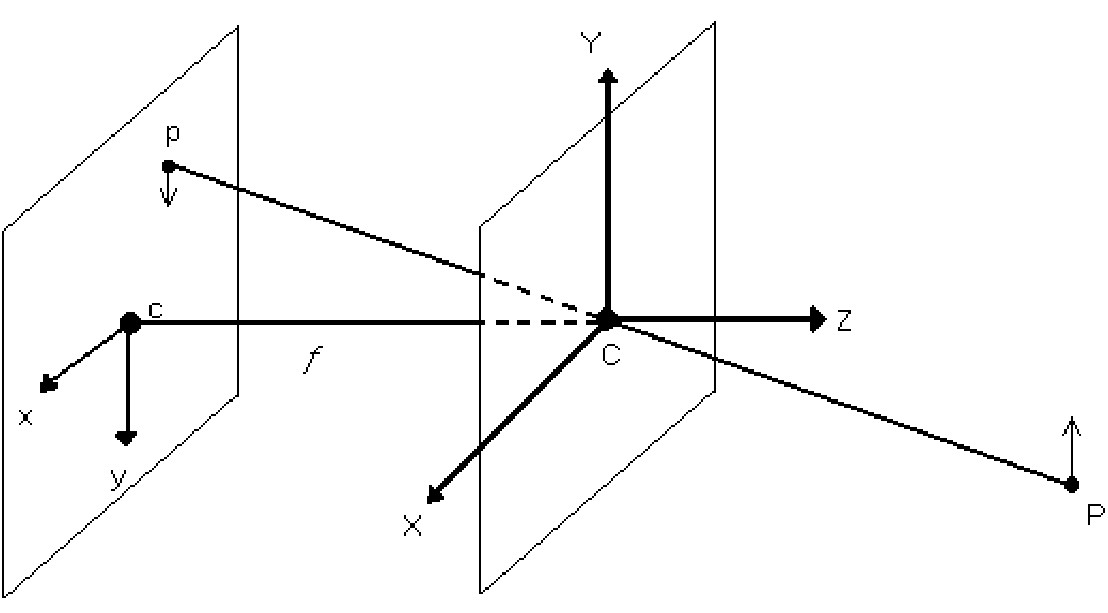
| + | |[[Image:Pinhole.png|thumb|200px|Pinhole camera model]] | ||
| + | |- | ||
| + | |[[Image:Julien1.jpg|thumb|200px|Calibration introduced to the [[MMVL]] by ''Julien Faucher'', ERASMUS exchange student from France]] | ||
| + | |- | ||
| + | |} | ||
=Calibration= | =Calibration= | ||
| − | == | + | ==Plane-to-camera homography== |
Let <math>\vec{m}_i\in\mathbb{R}^3,\,i\in\{1,2,\ldots,N\}</math> be the [http://en.wikipedia.org/wiki/Homogeneous_coordinates#Use_in_computer_graphics homogeneous coordinate] of the <math>i</math>th point on the planar calibration-object and let <math>\vec{m}^\prime_i\in\mathbb{R}^3</math> be the homogeneous coordinate of the corresponding pixel in the camera-image. Further let <math>(\mathbb{R}^n,\simeq)</math> be an [http://en.wikipedia.org/wiki/Equivalence_relation equivalence relation] defined by | Let <math>\vec{m}_i\in\mathbb{R}^3,\,i\in\{1,2,\ldots,N\}</math> be the [http://en.wikipedia.org/wiki/Homogeneous_coordinates#Use_in_computer_graphics homogeneous coordinate] of the <math>i</math>th point on the planar calibration-object and let <math>\vec{m}^\prime_i\in\mathbb{R}^3</math> be the homogeneous coordinate of the corresponding pixel in the camera-image. Further let <math>(\mathbb{R}^n,\simeq)</math> be an [http://en.wikipedia.org/wiki/Equivalence_relation equivalence relation] defined by | ||
| Line 51: | Line 59: | ||
<math> | <math> | ||
\begin{pmatrix} | \begin{pmatrix} | ||
| − | m_{i1}&m_{i2}&1&0&0&0&m^\prime_{i1}\,m_{i1}&m^\prime_{i1}\,m_{i2}&m^\prime_{i1}\\ | + | m_{i1}&m_{i2}&1&0&0&0&-m^\prime_{i1}\,m_{i1}&-m^\prime_{i1}\,m_{i2}&-m^\prime_{i1}\\ |
| − | 0&0&0&m_{i1}&m_{i2}&1&m^\prime_{i2}\,m_{i1}&m^\prime_{i2}\,m_{i2}&m^\prime_{i2} | + | 0&0&0&m_{i1}&m_{i2}&1&-m^\prime_{i2}\,m_{i1}&-m^\prime_{i2}\,m_{i2}&-m^\prime_{i2} |
\end{pmatrix}\, | \end{pmatrix}\, | ||
\begin{pmatrix}h_{11}\\h_{12}\\\vdots\\h_{33}\end{pmatrix}= | \begin{pmatrix}h_{11}\\h_{12}\\\vdots\\h_{33}\end{pmatrix}= | ||
| Line 61: | Line 69: | ||
<math> | <math> | ||
\underbrace{\begin{pmatrix} | \underbrace{\begin{pmatrix} | ||
| − | m_{11}&m_{12}&1&0&0&0&m^\prime_{11}\,m_{11}&m^\prime_{11}\,m_{12}&m^\prime_{11}\\ | + | m_{11}&m_{12}&1&0&0&0&-m^\prime_{11}\,m_{11}&-m^\prime_{11}\,m_{12}&-m^\prime_{11}\\ |
| − | 0&0&0&m_{11}&m_{12}&1&m^\prime_{12}\,m_{11}&m^\prime_{12}\,m_{12}&m^\prime_{12}\\ | + | 0&0&0&m_{11}&m_{12}&1&-m^\prime_{12}\,m_{11}&-m^\prime_{12}\,m_{12}&-m^\prime_{12}\\ |
| − | m_{21}&m_{22}&1&0&0&0&m^\prime_{21}\,m_{21}&m^\prime_{21}\,m_{22}&m^\prime_{21}\\ | + | m_{21}&m_{22}&1&0&0&0&-m^\prime_{21}\,m_{21}&-m^\prime_{21}\,m_{22}&-m^\prime_{21}\\ |
| − | 0&0&0&m_{21}&m_{22}&1&m^\prime_{22}\,m_{21}&m^\prime_{22}\,m_{22}&m^\prime_{22}\\ | + | 0&0&0&m_{21}&m_{22}&1&-m^\prime_{22}\,m_{21}&-m^\prime_{22}\,m_{22}&-m^\prime_{22}\\ |
\vdots&\vdots&\vdots&\vdots&\vdots&\vdots&\vdots&\vdots&\vdots\\ | \vdots&\vdots&\vdots&\vdots&\vdots&\vdots&\vdots&\vdots&\vdots\\ | ||
| − | m_{N1}&m_{N2}&1&0&0&0&m^\prime_{N1}\,m_{N1}&m^\prime_{N1}\,m_{N2}&m^\prime_{N1}\\ | + | m_{N1}&m_{N2}&1&0&0&0&-m^\prime_{N1}\,m_{N1}&-m^\prime_{N1}\,m_{N2}&-m^\prime_{N1}\\ |
| − | 0&0&0&m_{N1}&m_{N2}&1&m^\prime_{N2}\,m_{N1}&m^\prime_{N2}\,m_{N2}&m^\prime_{N2} | + | 0&0&0&m_{N1}&m_{N2}&1&-m^\prime_{N2}\,m_{N1}&-m^\prime_{N2}\,m_{N2}&-m^\prime_{N2} |
\end{pmatrix}}_{=:\mathcal{M}}\, | \end{pmatrix}}_{=:\mathcal{M}}\, | ||
\underbrace{\begin{pmatrix}h_{11}\\h_{12}\\\vdots\\h_{33}\end{pmatrix}}_{=:\vec{h}}= | \underbrace{\begin{pmatrix}h_{11}\\h_{12}\\\vdots\\h_{33}\end{pmatrix}}_{=:\vec{h}}= | ||
| Line 82: | Line 90: | ||
<math>\widehat{\vec{h}}</math> can be computed using the [http://en.wikipedia.org/wiki/Singular_value_decomposition Singular value decomposition] <math>\mathcal{M}=\mathcal{U}\,\Sigma\,\mathcal{V}^*</math>, because these are the properties of the right handed singular vector <math>\vec{v}_1</math> with the smallest singular value <math>\sigma_1</math> (where <math>\mathcal{V}=\big(\vec{v}_1\,\vec{v}_2\,\cdots\big)</math>). I.e. <math>\widehat{\vec{h}}=\vec{v}_1</math>. | <math>\widehat{\vec{h}}</math> can be computed using the [http://en.wikipedia.org/wiki/Singular_value_decomposition Singular value decomposition] <math>\mathcal{M}=\mathcal{U}\,\Sigma\,\mathcal{V}^*</math>, because these are the properties of the right handed singular vector <math>\vec{v}_1</math> with the smallest singular value <math>\sigma_1</math> (where <math>\mathcal{V}=\big(\vec{v}_1\,\vec{v}_2\,\cdots\big)</math>). I.e. <math>\widehat{\vec{h}}=\vec{v}_1</math>. | ||
| − | [[Image:working.gif]] Under construction ... | + | Knowing the homography <math>\mathcal{H}</math> already is sufficient for the [[Interactive Camera-Projector System]]. |
| + | |||
| + | ==Intrinsic and extrinsic camera parameters== | ||
| + | Please see references below ... | ||
| + | <!-- [[Image:working.gif]] Under construction ... --> | ||
=See Also= | =See Also= | ||
* [[Mimas]] | * [[Mimas]] | ||
| + | * [[Bright]] : A project using the camera calibration to build a laser-line based 3-D scanner. | ||
* [[Interactive Camera-Projector System]] | * [[Interactive Camera-Projector System]] | ||
=External Links= | =External Links= | ||
| − | * [http://research.microsoft.com/%7Ezhang/Calib/ A Flexible New Technique for Camera Calibration] | + | * [http://vision.eng.shu.ac.uk/manuel/bright/report_faucher.pdf Julien Faucher's report] |
| + | * [http://research.microsoft.com/%7Ezhang/Calib/ Zhengyou Zhang: A Flexible New Technique for Camera Calibration] | ||
| + | * [http://homepages.inf.ed.ac.uk/rbf/BOOKS/BANDB/bandb.htm Ballard and Brown: Computer vision (chapter A1.8.1 on camera calibration)] | ||
| + | * [http://video.google.co.uk/videoplay?docid=-6642378035529869995#9m43s Augmented Reality with Sony Playstation (google video)] | ||
| + | * [http://www.vision.caltech.edu/bouguetj/calib_doc/ Camera calibration toolbox for Matlab] | ||
| + | * [http://research.graphicon.ru/calibration/gml-c-camera-calibration-toolbox.html GML Camera Calibration toolbox] | ||
| + | * [http://cvlab.epfl.ch/software/bazar/calib.php EPFL camera calibration software] | ||
| + | * [http://www.youtube.com/watch?v=BkZkq6zPwQM&feature=player_embedded#! MRPT camera calibration software] | ||
| + | * [http://opencv.willowgarage.com/documentation/python/camera_calibration_and_3d_reconstruction.html OpenCV / WillowGarage camera calibration] | ||
| + | |||
| + | {{Addthis}} | ||
[[Category:Projects]] | [[Category:Projects]] | ||
| − | [[Category: | + | [[Category:Fun-Projects]] |
Latest revision as of 17:08, 15 June 2010
 Prototype low-cost platform for 3D reconstruction of objects using laser-triangulation (10 MByte video) |
 Calibration introduced to the MMVL by Julien Faucher, ERASMUS exchange student from France |
Contents |
[edit] Calibration
[edit] Plane-to-camera homography
Let <math>\vec{m}_i\in\mathbb{R}^3,\,i\in\{1,2,\ldots,N\}</math> be the homogeneous coordinate of the <math>i</math>th point on the planar calibration-object and let <math>\vec{m}^\prime_i\in\mathbb{R}^3</math> be the homogeneous coordinate of the corresponding pixel in the camera-image. Further let <math>(\mathbb{R}^n,\simeq)</math> be an equivalence relation defined by
<math> \vec{a}\simeq\vec{b}\ :\Leftrightarrow\ \exists\lambda\in\mathbb{R}/\{0\}:\,\lambda\,\vec{a}=\vec{b} </math>
If the camera-system does an ideal central projection (e.g. no distortion), the projective transformation (the Homography) can be modelled using <math>\mathcal{H}\in\mathbb{R}^{3\times 3}</math> as follows
<math> \vec{m^\prime}_i+\vec{\epsilon}_i\simeq\mathcal{H}\vec{m}_i </math>
or more elaborately <math> \lambda\,\begin{pmatrix}m^\prime_{i1}\\m^\prime_{i2}\\m^\prime_{i3}\end{pmatrix}+ \begin{pmatrix}\epsilon_{i1}\\\epsilon_{i2}\\\epsilon_{i3}\end{pmatrix}= \begin{pmatrix}h_{11}&h_{12}&h_{13}\\h_{21}&h_{22}&h_{23}\\h_{31}&h_{32}&h_{33}\end{pmatrix}\, \begin{pmatrix}m_{i1}\\m_{i2}\\m_{i3}\end{pmatrix} </math> where <math>(\epsilon_{i1},\epsilon_{i2})^\top</math> is the zero-mean error-vector in the observation of the <math>i</math>th point in the camera-image.
Using <math>m_{i3}=m^\prime_{i3}=1,\ \epsilon_{i3}=0</math> and <math>\vec{h_i}^\top=\begin{pmatrix}h_{i1}&h_{i2}&h_{i3}\end{pmatrix},\ i\in\{1,2,3\}</math> the model can be reformulated to <math> \begin{pmatrix}m^\prime_{i1}\\m^\prime_{i2}\end{pmatrix}=\cfrac{1}{\vec{h_3}^\top\cdot\vec{m}_i}\, \begin{pmatrix}\vec{h_1}^\top\\\vec{h_2}^\top\end{pmatrix}\, \begin{pmatrix}m_{i1}\\m_{i2}\\1\end{pmatrix}- \begin{pmatrix}\epsilon_{i1}\\\epsilon_{i2}\end{pmatrix} </math> or <math> \begin{pmatrix}m^\prime_{i1}\\m^\prime_{i2}\end{pmatrix}\,\big(\vec{h_3}^\top\cdot\vec{m}_i\big)= \begin{pmatrix}\vec{h_1}^\top\\\vec{h_2}^\top\end{pmatrix}\, \begin{pmatrix}m_{i1}\\m_{i2}\\1\end{pmatrix}- \begin{pmatrix}\epsilon^\prime_{i1}\\\epsilon^\prime_{i2}\end{pmatrix} </math> with <math>\vec{\epsilon^\prime}_i=\big[\vec{h_3}^\top\cdot\vec{m}_i\big]\,\vec{\epsilon}_i</math> and using <math>|\mathcal{H}|\neq 0</math>
It is assumed, that the vectors <math>\vec{\epsilon^\prime}_i</math> have equal variances (i.e. <math>\vec{h_3}^\top\cdot\vec{m}_1\approx\vec{h_3}^\top\cdot\vec{m}_2\approx\ldots</math>) so that the Gauss-Markov theorem can be applied using <math>(\epsilon^\prime_{i1},\epsilon^\prime_{i2})^\top</math> as error-vectors. In this case the miminum least-squares estimator is the best linear estimator.
Each point-pair yields the following system of two linear equations <math> \begin{pmatrix}h_{11}\,m_{i1}+h_{12}\,m_{i2}+h_{13}\\h_{21}\,m_{i1}+h_{22}\,m_{i2}+h_{23}\end{pmatrix}- \begin{pmatrix}m^\prime_{i1}\,m_{i1}\,h_{31}+m^\prime_{i1}\,m_{i2}\,h_{32}+m^\prime_{i1}\,h_{33}\\ m^\prime_{i2}\,m_{i1}\,h_{31}+m^\prime_{i2}\,m_{i2}\,h_{32}+m^\prime_{i2}\,h_{33}\end{pmatrix}= \begin{pmatrix}\epsilon^\prime_{i1}\\\epsilon^\prime_{i2}\end{pmatrix} </math>
Isolating the elements of the unknown matrix <math>\mathcal{H}</math> gives <math> \begin{pmatrix} m_{i1}&m_{i2}&1&0&0&0&-m^\prime_{i1}\,m_{i1}&-m^\prime_{i1}\,m_{i2}&-m^\prime_{i1}\\ 0&0&0&m_{i1}&m_{i2}&1&-m^\prime_{i2}\,m_{i1}&-m^\prime_{i2}\,m_{i2}&-m^\prime_{i2} \end{pmatrix}\, \begin{pmatrix}h_{11}\\h_{12}\\\vdots\\h_{33}\end{pmatrix}= \begin{pmatrix}\epsilon^\prime_{i1}\\\epsilon^\prime_{i2}\end{pmatrix} </math>
The combined system of all linear equations is <math> \underbrace{\begin{pmatrix} m_{11}&m_{12}&1&0&0&0&-m^\prime_{11}\,m_{11}&-m^\prime_{11}\,m_{12}&-m^\prime_{11}\\ 0&0&0&m_{11}&m_{12}&1&-m^\prime_{12}\,m_{11}&-m^\prime_{12}\,m_{12}&-m^\prime_{12}\\ m_{21}&m_{22}&1&0&0&0&-m^\prime_{21}\,m_{21}&-m^\prime_{21}\,m_{22}&-m^\prime_{21}\\ 0&0&0&m_{21}&m_{22}&1&-m^\prime_{22}\,m_{21}&-m^\prime_{22}\,m_{22}&-m^\prime_{22}\\ \vdots&\vdots&\vdots&\vdots&\vdots&\vdots&\vdots&\vdots&\vdots\\ m_{N1}&m_{N2}&1&0&0&0&-m^\prime_{N1}\,m_{N1}&-m^\prime_{N1}\,m_{N2}&-m^\prime_{N1}\\ 0&0&0&m_{N1}&m_{N2}&1&-m^\prime_{N2}\,m_{N1}&-m^\prime_{N2}\,m_{N2}&-m^\prime_{N2} \end{pmatrix}}_{=:\mathcal{M}}\, \underbrace{\begin{pmatrix}h_{11}\\h_{12}\\\vdots\\h_{33}\end{pmatrix}}_{=:\vec{h}}= \begin{pmatrix}\epsilon^\prime_{11}\\\epsilon^\prime_{12}\\\epsilon^\prime_{21}\\\epsilon^\prime_{22}\\ \vdots\\\epsilon^\prime_{N1}\\\epsilon^\prime_{N2}\end{pmatrix} </math>
To avoid the trivial solution <math>\vec{h}=\vec{0}</math> the constraint <math>||\vec{h}||=1</math> is introduced without loss of generality.
The calibration problem now has been reduced to the problem of finding <math>\widehat{\vec{h}}\in\mathbb{R}^9</math> such that
- <math>||\mathcal{M}\,\widehat{\vec{h}}||</math> is minimal and
- <math>||\widehat{\vec{h}}||=1</math>
<math>\widehat{\vec{h}}</math> can be computed using the Singular value decomposition <math>\mathcal{M}=\mathcal{U}\,\Sigma\,\mathcal{V}^*</math>, because these are the properties of the right handed singular vector <math>\vec{v}_1</math> with the smallest singular value <math>\sigma_1</math> (where <math>\mathcal{V}=\big(\vec{v}_1\,\vec{v}_2\,\cdots\big)</math>). I.e. <math>\widehat{\vec{h}}=\vec{v}_1</math>.
Knowing the homography <math>\mathcal{H}</math> already is sufficient for the Interactive Camera-Projector System.
[edit] Intrinsic and extrinsic camera parameters
Please see references below ...
[edit] See Also
- Mimas
- Bright : A project using the camera calibration to build a laser-line based 3-D scanner.
- Interactive Camera-Projector System
[edit] External Links
- Julien Faucher's report
- Zhengyou Zhang: A Flexible New Technique for Camera Calibration
- Ballard and Brown: Computer vision (chapter A1.8.1 on camera calibration)
- Augmented Reality with Sony Playstation (google video)
- Camera calibration toolbox for Matlab
- GML Camera Calibration toolbox
- EPFL camera calibration software
- MRPT camera calibration software
- OpenCV / WillowGarage camera calibration