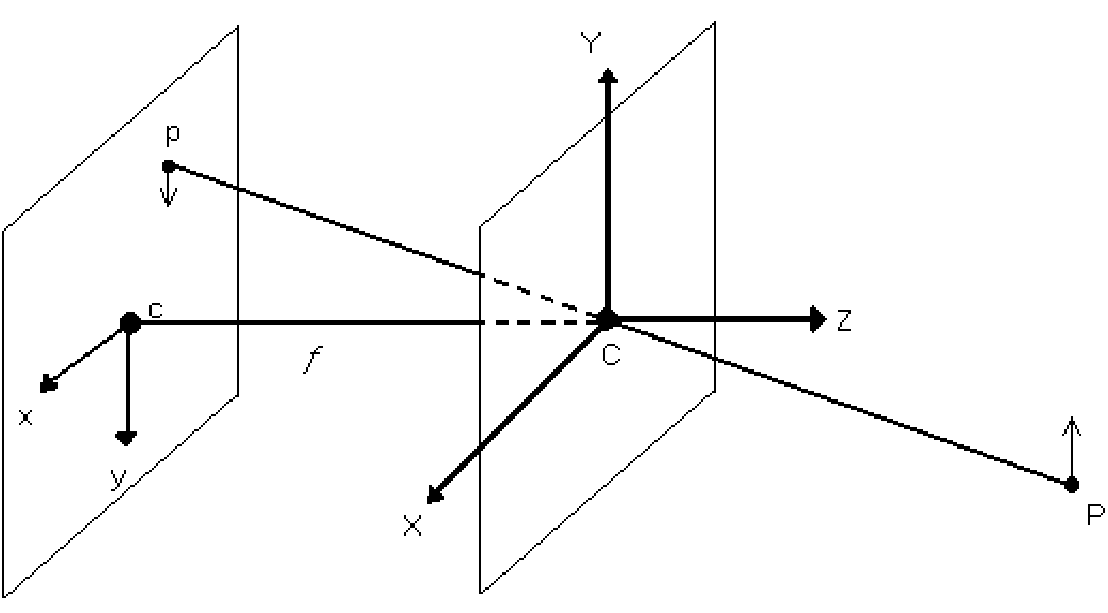
Mimas Camera Calibration
 |
 |
 |
Contents |
Calibration
Distortion-free Camera
Let <math>\vec{m}_i\in\mathbb{R}^3,\,i\in\{1,2,\ldots,N\}</math> be the homogeneous coordinate of the <math>i</math>th point on the planar calibration-object and let <math>\vec{m}^\prime_i\in\mathbb{R}^3</math> be the homogeneous coordinate of the corresponding pixel in the camera-image. Further let <math>(\mathbb{R}^n,\simeq)</math> be an equivalence relation defined by
<math> \vec{a}\simeq\vec{b}\ :\Leftrightarrow\ \exists\lambda\in\mathbb{R}/\{0\}:\,\lambda\,\vec{a}=\vec{b} </math>
If the camera-system does an ideal central projection (e.g. no distortion), the projective transformation (the Homography) can be modelled using <math>\mathcal{H}\in\mathbb{R}^{3\times 3}</math> as follows
<math> \vec{m^\prime}_i+\vec{\epsilon}_i\simeq\mathcal{H}\vec{m}_i </math>
or more elaborately <math> \lambda\,\begin{pmatrix}m^\prime_{i1}\\m^\prime_{i2}\\m^\prime_{i3}\end{pmatrix}+ \begin{pmatrix}\epsilon_{i1}\\\epsilon_{i2}\\\epsilon_{i3}\end{pmatrix}= \begin{pmatrix}h_{11}&h_{12}&h_{13}\\h_{21}&h_{22}&h_{23}\\h_{31}&h_{32}&h_{33}\end{pmatrix}\, \begin{pmatrix}m_{i1}\\m_{i2}\\m_{i3}\end{pmatrix} </math> where <math>(\epsilon_{i1},\epsilon_{i2})^\top</math> is the zero-mean error-vector in the observation of the <math>i</math>th point in the camera-image.
Using <math>m_{i3}=m^\prime_{i3}=1,\ \epsilon_{i3}=0</math> and <math>\vec{h_i}^\top=\begin{pmatrix}h_{i1}&h_{i2}&h_{i3}\end{pmatrix},\ i\in\{1,2,3\}</math> the model can be reformulated to <math> \begin{pmatrix}m^\prime_{i1}\\m^\prime_{i2}\end{pmatrix}=\cfrac{1}{\vec{h_3}^\top\cdot\vec{m}_i}\, \begin{pmatrix}\vec{h_1}^\top\\\vec{h_2}^\top\end{pmatrix}\, \begin{pmatrix}m_{i1}\\m_{i2}\\1\end{pmatrix}- \begin{pmatrix}\epsilon_{i1}\\\epsilon_{i2}\end{pmatrix} </math> or <math> \begin{pmatrix}m^\prime_{i1}\\m^\prime_{i2}\end{pmatrix}\,\big(\vec{h_3}^\top\cdot\vec{m}_i\big)= \begin{pmatrix}\vec{h_1}^\top\\\vec{h_2}^\top\end{pmatrix}\, \begin{pmatrix}m_{i1}\\m_{i2}\\1\end{pmatrix}- \begin{pmatrix}\epsilon^\prime_{i1}\\\epsilon^\prime_{i2}\end{pmatrix} </math> with <math>\vec{\epsilon^\prime}_i=\big[\vec{h_3}^\top\cdot\vec{m}_i\big]\,\vec{\epsilon}_i</math> and using <math>|\mathcal{H}|\neq 0</math>
It is assumed, that the vectors <math>\vec{\epsilon^\prime}_i</math> have equal variances (i.e. <math>\vec{h_3}^\top\cdot\vec{m}_1\approx\vec{h_3}^\top\cdot\vec{m}_2\approx\ldots</math>) so that the Gauss-Markov theorem can be applied using <math>(\epsilon^\prime_{i1},\epsilon^\prime_{i2})^\top</math> as error-vectors. In this case the miminum least-squares estimator is the best linear estimator.
Each point-pair yields the following system of two linear equations <math> \begin{pmatrix}h_{11}\,m_{i1}+h_{12}\,m_{i2}+h_{13}\\h_{21}\,m_{i1}+h_{22}\,m_{i2}+h_{23}\end{pmatrix}- \begin{pmatrix}m^\prime_{i1}\,m_{i1}\,h_{31}+m^\prime_{i1}\,m_{i2}\,h_{32}+m^\prime_{i1}\,h_{33}\\ m^\prime_{i2}\,m_{i1}\,h_{31}+m^\prime_{i2}\,m_{i2}\,h_{32}+m^\prime_{i2}\,h_{33}\end{pmatrix}= \begin{pmatrix}\epsilon^\prime_{i1}\\\epsilon^\prime_{i2}\end{pmatrix} </math>
Isolating the elements of the unknown matrix <math>\mathcal{H}</math> gives <math> \begin{pmatrix} m_{i1}&m_{i2}&1&0&0&0&m^\prime_{i1}\,m_{i1}&m^\prime_{i1}\,m_{i2}&m^\prime_{i1}\\ 0&0&0&m_{i1}&m_{i2}&1&m^\prime_{i2}\,m_{i1}&m^\prime_{i2}\,m_{i2}&m^\prime_{i2} \end{pmatrix}\, \begin{pmatrix}h_{11}\\h_{12}\\\vdots\\h_{33}\end{pmatrix}= \begin{pmatrix}\epsilon^\prime_{i1}\\\epsilon^\prime_{i2}\end{pmatrix} </math>
The combined system of all linear equations is <math> \underbrace{\begin{pmatrix} m_{11}&m_{12}&1&0&0&0&m^\prime_{11}\,m_{11}&m^\prime_{11}\,m_{12}&m^\prime_{11}\\ 0&0&0&m_{11}&m_{12}&1&m^\prime_{12}\,m_{11}&m^\prime_{12}\,m_{12}&m^\prime_{12}\\ m_{21}&m_{22}&1&0&0&0&m^\prime_{21}\,m_{21}&m^\prime_{21}\,m_{22}&m^\prime_{21}\\ 0&0&0&m_{21}&m_{22}&1&m^\prime_{22}\,m_{21}&m^\prime_{22}\,m_{22}&m^\prime_{22}\\ \vdots&\vdots&\vdots&\vdots&\vdots&\vdots&\vdots&\vdots&\vdots\\ m_{N1}&m_{N2}&1&0&0&0&m^\prime_{N1}\,m_{N1}&m^\prime_{N1}\,m_{N2}&m^\prime_{N1}\\ 0&0&0&m_{N1}&m_{N2}&1&m^\prime_{N2}\,m_{N1}&m^\prime_{N2}\,m_{N2}&m^\prime_{N2} \end{pmatrix}}_{=:\mathcal{M}}\, \underbrace{\begin{pmatrix}h_{11}\\h_{12}\\\vdots\\h_{33}\end{pmatrix}}_{=:\vec{h}}= \begin{pmatrix}\epsilon^\prime_{11}\\\epsilon^\prime_{12}\\\epsilon^\prime_{21}\\\epsilon^\prime_{22}\\ \vdots\\\epsilon^\prime_{N1}\\\epsilon^\prime_{N2}\end{pmatrix} </math>
To avoid the trivial solution <math>\vec{h}=\vec{0}</math> the constraint <math>||\vec{h}||=1</math> is introduced without loss of generality.
The calibration problem now has been reduced to the problem of finding <math>\widehat{\vec{h}}\in\mathbb{R}^9</math> such that
- <math>||\mathcal{M}\,\widehat{\vec{h}}||</math> is minimal and
- <math>||\widehat{\vec{h}}||=1</math>
<math>\widehat{\vec{h}}</math> can be computed using the Singular value decomposition <math>\mathcal{M}=\mathcal{U}\,\Sigma\,\mathcal{V}^*</math>, because these are the properties of the right handed singular vector <math>\vec{v}_1</math> with the smallest singular value <math>\sigma_1</math> (where <math>\mathcal{V}=\big(\vec{v}_1\,\vec{v}_2\,\cdots\big)</math>). I.e. <math>\widehat{\vec{h}}=\vec{v}_1</math>.
Under construction ...
