
|
Collaboration diagram for Lapack functions:

|
Classes | |
| struct | mimas::gglse_t< T > |
| Function-object for gglse. More... | |
| struct | mimas::inv_t< T > |
| Function-object for inv. More... | |
| struct | mimas::gels_t< T > |
| Function-object for gels. More... | |
| struct | mimas::gesvd_t< T > |
| Function-object for gesvd. More... | |
| struct | mimas::gesdd_t< T > |
| Function-wrapper for gesdd. More... | |
| struct | mimas::syev_t< T > |
| Function-wrapper for syev. More... | |
| struct | mimas::pptrf_t< T > |
| Function-object for pptrf. More... | |
Functions | |
| template<typename T> | |
| boost::numeric::ublas::vector< T > | mimas::gglse (const boost::numeric::ublas::matrix< T, boost::numeric::ublas::column_major > &A, const boost::numeric::ublas::matrix< T, boost::numeric::ublas::column_major > &B, const boost::numeric::ublas::vector< T > &c, const boost::numeric::ublas::vector< T > &d) |
| Solve the linear equality-constrained least squares (LSE) problem. | |
| template<typename T> | |
| boost::numeric::ublas::matrix< T, boost::numeric::ublas::column_major > | mimas::inv (const boost::numeric::ublas::matrix< T, boost::numeric::ublas::column_major > &A) |
| Compute matrix inverse by using LU factorization. | |
| template<typename T> | |
| boost::numeric::ublas::vector< T > | mimas::gels (const boost::numeric::ublas::matrix< T, boost::numeric::ublas::column_major > &A, const boost::numeric::ublas::vector< T > &b) |
| solve overdetermined linear systems using QR factorization. | |
| template<typename T> | |
| boost::numeric::ublas::banded_matrix< T > | mimas::gesvd (const boost::numeric::ublas::matrix< T, boost::numeric::ublas::column_major > &A, boost::numeric::ublas::matrix< T, boost::numeric::ublas::column_major > *U, boost::numeric::ublas::matrix< T, boost::numeric::ublas::column_major > *Vt) |
| Compute the singular value decomposition (SVD) of a matrix A. | |
| template<typename T> | |
| boost::numeric::ublas::banded_matrix< T > | mimas::gesdd (const boost::numeric::ublas::matrix< T, boost::numeric::ublas::column_major > &A, boost::numeric::ublas::matrix< T, boost::numeric::ublas::column_major > *U, boost::numeric::ublas::matrix< T, boost::numeric::ublas::column_major > *Vt) |
| Compute the singular value decomposition (SVD) of a matrix A (fast). | |
| template<typename T> | |
| boost::numeric::ublas::diagonal_matrix< T > | mimas::syev (const boost::numeric::ublas::symmetric_matrix< T, boost::numeric::ublas::upper > &A, boost::numeric::ublas::matrix< T, boost::numeric::ublas::column_major > *E) |
| Compute all eigenvalues and, optionally, eigenvectors of a real symmetric matrix A. | |
| template<typename T> | |
| boost::numeric::ublas::triangular_matrix< T, boost::numeric::ublas::upper, boost::numeric::ublas::column_major > | mimas::pptrf (const boost::numeric::ublas::symmetric_matrix< T, boost::numeric::ublas::upper, boost::numeric::ublas::column_major > &A) |
| Compute the Cholesky decomposition of a symmetric matrix A. | |
The matrix- and vector-classes of boost are used as datatypes.
Note, that lapack uses matrices in column-major orientation. You are forced to convert to
boost::numeric::ublas::matrix< T, boost::numeric::ublas::column_major >
| boost::numeric::ublas::vector< T > mimas::gels | ( | const boost::numeric::ublas::matrix< T, boost::numeric::ublas::column_major > & | A, | |
| const boost::numeric::ublas::vector< T > & | b | |||
| ) |
solve overdetermined linear systems using QR factorization.
Solve the minimum least square problem. 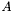 and
and 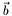 are given and
are given and 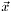 is the desired solution for
is the desired solution for
![\[\vec{x}:=\displaystyle\mathop{argmin}_{\vec{x}}|\vec{b}-A\,\vec{x}|\]](form_29.png)
This is much faster than computing 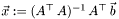 with the matrix-classes.
with the matrix-classes.
See manpage dgels(1) for more documentation. The parametrisation for underdetermined systems wasn't working as expected and was not included in the interface therefore.
| boost::numeric::ublas::banded_matrix< T > mimas::gesdd | ( | const boost::numeric::ublas::matrix< T, boost::numeric::ublas::column_major > & | A, | |
| boost::numeric::ublas::matrix< T, boost::numeric::ublas::column_major > * | U, | |||
| boost::numeric::ublas::matrix< T, boost::numeric::ublas::column_major > * | Vt | |||
| ) |
Compute the singular value decomposition (SVD) of a matrix A (fast).
Same as mimas::gesvd but faster algorithm (divide-and-conquer approach).
Note that the singular value decomposition doesn't necessarily converge. In the later case an exception is thrown.
See manpage dgesdd(1) for more documentation.
Note, that, in contrast to the interface of mimas::gesvd, U and Vt must both be defined or both be NULL!
| A | Matrix to be decomposed. | |
| U | Returns matrix with left hand singular vectors 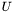 (may be (may be NULL, if it is of no interest). | |
| Vt | Returns transposed matrix with right hand singular vectors `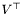 (may be (may be NULL, if it is of no interest). |
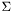 .
. | boost::numeric::ublas::banded_matrix< T > mimas::gesvd | ( | const boost::numeric::ublas::matrix< T, boost::numeric::ublas::column_major > & | A, | |
| boost::numeric::ublas::matrix< T, boost::numeric::ublas::column_major > * | U, | |||
| boost::numeric::ublas::matrix< T, boost::numeric::ublas::column_major > * | Vt | |||
| ) |
Compute the singular value decomposition (SVD) of a matrix A.
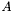 is given.
is given. 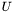 ,
, 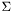 and
and 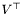 have to be determined, such that:
have to be determined, such that: 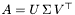 and
and 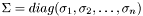 diagonal matrix with the singular values
diagonal matrix with the singular values 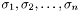 (
(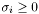 ) in descending order. The singular values are sorted in descending order.
) in descending order. The singular values are sorted in descending order.
Note that the singular value decomposition doesn't necessarily converge. In the later case an exception is thrown.
See mimas::gesdd, which is a faster algorithm.
See manpage dgesvd(1) for more documentation.
| A | Matrix to be decomposed. | |
| U | Returns matrix with left hand singular vectors 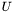 (may be (may be NULL, if it is of no interest). | |
| Vt | Returns transposed matrix with right hand singular vectors 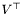 (may be (may be NULL, if it is of no interest). |
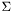 .
.| boost::numeric::ublas::vector< T > mimas::gglse | ( | const boost::numeric::ublas::matrix< T, boost::numeric::ublas::column_major > & | A, | |
| const boost::numeric::ublas::matrix< T, boost::numeric::ublas::column_major > & | B, | |||
| const boost::numeric::ublas::vector< T > & | c, | |||
| const boost::numeric::ublas::vector< T > & | d | |||
| ) |
| boost::numeric::ublas::matrix< T, boost::numeric::ublas::column_major > mimas::inv | ( | const boost::numeric::ublas::matrix< T, boost::numeric::ublas::column_major > & | A | ) |
| boost::numeric::ublas::triangular_matrix< T, boost::numeric::ublas::upper, boost::numeric::ublas::column_major > mimas::pptrf | ( | const boost::numeric::ublas::symmetric_matrix< T, boost::numeric::ublas::upper, boost::numeric::ublas::column_major > & | A | ) |
Compute the Cholesky decomposition of a symmetric matrix A.
Given a symmetric positive-definite matrix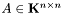 , the Cholesky decomposition returns the upper triangular matrix
, the Cholesky decomposition returns the upper triangular matrix 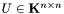 such that:
such that:
![\[A=U^\top\,U\]](form_45.png)
| A | Symmetric matrix (with upper and column-based storage) to compute Cholesky decomposition for. |
| boost::numeric::ublas::diagonal_matrix< T > mimas::syev | ( | const boost::numeric::ublas::symmetric_matrix< T, boost::numeric::ublas::upper > & | A, | |
| boost::numeric::ublas::matrix< T, boost::numeric::ublas::column_major > * | E | |||
| ) |
Compute all eigenvalues and, optionally, eigenvectors of a real symmetric matrix A.
The eigenvalues and eigenvectors of a symmetric matrix 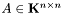 can be computed.
can be computed.
The eigenvectors are orthogonal by nature and normalised by definition. If the matrix 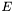 contains the eigenvectors of
contains the eigenvectors of 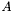 , then the eigentransform can be written as (
, then the eigentransform can be written as (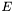 is orthonormal
is orthonormal 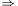
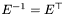 ):
):
![\[A=E\,\Lambda\,E^\top\]](form_41.png)
Where 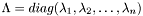 is a diagonal matrix with the eigenvalues
is a diagonal matrix with the eigenvalues 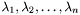 in ascending order.
in ascending order.
See manpage dsyev(1) for more documentation.
Compute eigenvalues and, optionally, the eigenvectors of A.
| A | Symmetric matrix (with upper storage) to compute eigentransform for. | |
| E | Pointer to matrix, where the eigenvectors have to be written to (may be NULL, if it is of no interest). |