From MMVLWiki

Table of contents

1 Introduction 2 Implementation 3 Example 4 See Also 5 External Links

Introduction

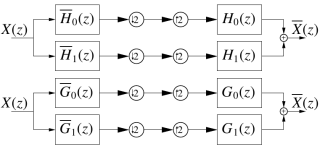
Complex wavelet analysis requires two Hilbert-pairs of wavelets. A Hilbert-pair of wavelets consists of two wavelets which have a phase-shift of 90° to each other. The two Hilbert-pairs are designed to form a filter bank to decompose the signal into high and low frequencies. The to Hilbert-pairs can be designed to also fulfil the perfect-reconstruction condition. Selesnick (https://taco.poly.edu/selesi/) has developed a method for designing Hilbert transform pairs of biorthogonal wavelet bases.

Implementation

The implementation is part of HornetsEye. Since the Ruby code is stand-alone you can download it here if you do not want to download the whole HornetsEye package: selesnick.rb (https://vision.eng.shu.ac.uk/jan/selesnick.rb)

Example

Biorthogonal Hilbert-pairs of wavelet bases (k=ks=5,l=3)

Overview of the filter bank	H0	H1	G0	G1
	H0	H1	G0	G1

See Also

• HornetsEye
• Hypercomplex Wavelets

External Links

• Ivan Selesnick's homepage (https://taco.poly.edu/selesi/)
  • I. W. Selesnick: The design of approximate Hilbert transform pairs of wavelet bases (https://taco.poly.edu/selesi/pubs/HilbertPairTSP.pdf), IEEE Trans. on Signal Processing, 50(5):1144-1152, May 2002
• Nick Kingsbury's homepage (https://www-sigproc.eng.cam.ac.uk/~ngk/)
• Perfect Reconstruction (Nick Kingsbury) (https://cnx.org/content/m11136/latest/)