Mimas Camera Calibration

From MMVLWiki

Prototype low-cost platform for 3D reconstruction of objects using laser-triangulation (10 MByte video (http://vision.eng.shu.ac.uk/jan/reconstruction%20platform.avi))
Enlarge
Prototype low-cost platform for 3D reconstruction of objects using laser-triangulation (10 MByte video (http://vision.eng.shu.ac.uk/jan/reconstruction%20platform.avi))
Pinhole camera model
Enlarge
Pinhole camera model
Calibration introduced to the by Julien Faucher, ERASMUS exchange student from France
Enlarge
Calibration introduced to the MMVL by Julien Faucher, ERASMUS exchange student from France
Table of contents
1 Calibration

1.1 Plane-to-camera homography
1.2 Intrinsic and extrinsic camera parameters

2 See Also
3 External Links
[edit]

Calibration

[edit]

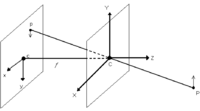
Plane-to-camera homography

Let 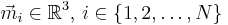\vec{m}_i\in\mathbb{R}^3,\,i\in\{1,2,\ldots,N\} be the homogeneous coordinate (http://en.wikipedia.org/wiki/Homogeneous_coordinates#Use_in_computer_graphics) of the ith point on the planar calibration-object and let 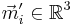\vec{m}^\prime_i\in\mathbb{R}^3 be the homogeneous coordinate of the corresponding pixel in the camera-image. Further let (\mathbb{R}^n,\simeq) be an equivalence relation (http://en.wikipedia.org/wiki/Equivalence_relation) defined by

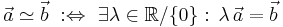
\vec{a}\simeq\vec{b}\ :\Leftrightarrow\ \exists\lambda\in\mathbb{R}/\{0\}:\,\lambda\,\vec{a}=\vec{b}

If the camera-system does an ideal central projection (e.g. no distortion), the projective transformation (the Homography (http://en.wikipedia.org/wiki/Homography)) can be modelled using 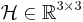\mathcal{H}\in\mathbb{R}^{3\times 3} as follows

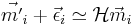
\vec{m^\prime}_i+\vec{\epsilon}_i\simeq\mathcal{H}\vec{m}_i

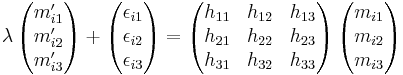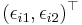or more elaborately \lambda\,\begin{pmatrix}m^\prime_{i1}\\m^\prime_{i2}\\m^\prime_{i3}\end{pmatrix}+ \begin{pmatrix}\epsilon_{i1}\\\epsilon_{i2}\\\epsilon_{i3}\end{pmatrix}= \begin{pmatrix}h_{11}&h_{12}&h_{13}\\h_{21}&h_{22}&h_{23}\\h_{31}&h_{32}&h_{33}\end{pmatrix}\, \begin{pmatrix}m_{i1}\\m_{i2}\\m_{i3}\end{pmatrix} where (\epsilon_{i1},\epsilon_{i2})^\top is the zero-mean error-vector in the observation of the ith point in the camera-image.

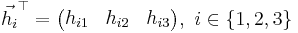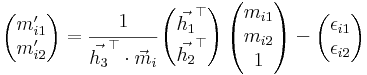Using m_{i3}=m^\prime_{i3}=1,\ \epsilon_{i3}=0 and \vec{h_i}^\top=\begin{pmatrix}h_{i1}&h_{i2}&h_{i3}\end{pmatrix},\ i\in\{1,2,3\} the model can be reformulated to \begin{pmatrix}m^\prime_{i1}\\m^\prime_{i2}\end{pmatrix}=\cfrac{1}{\vec{h_3}^\top\cdot\vec{m}_i}\, \begin{pmatrix}\vec{h_1}^\top\\\vec{h_2}^\top\end{pmatrix}\, \begin{pmatrix}m_{i1}\\m_{i2}\\1\end{pmatrix}- \begin{pmatrix}\epsilon_{i1}\\\epsilon_{i2}\end{pmatrix} or \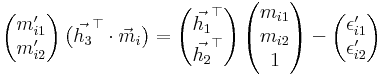begin{pmatrix}m^\prime_{i1}\\m^\prime_{i2}\end{pmatrix}\,\big(\vec{h_3}^\top\cdot\vec{m}_i\big)= \begin{pmatrix}\vec{h_1}^\top\\\vec{h_2}^\top\end{pmatrix}\, \begin{pmatrix}m_{i1}\\m_{i2}\\1\end{pmatrix}- \begin{pmatrix}\epsilon^\prime_{i1}\\\epsilon^\prime_{i2}\end{pmatrix} with \vec{\epsilon^\prime}_i=\big[\vec{h_3}^\top\cdot\vec{m}_i\big]\,\vec{\epsilon}_i and using |\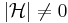mathcal{H}|\neq 0

It is assumed, that the vectors 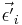\vec{\epsilon^\prime}_i have equal variances (i.e. 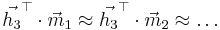\vec{h_3}^\top\cdot\vec{m}_1\approx\vec{h_3}^\top\cdot\vec{m}_2\approx\ldots) so that the Gauss-Markov theorem (http://en.wikipedia.org/wiki/Gauss-Markov_theorem) can be applied using 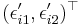(\epsilon^\prime_{i1},\epsilon^\prime_{i2})^\top as error-vectors. In this case the miminum least-squares estimator (http://en.wikipedia.org/wiki/Least_squares) is the best linear estimator.

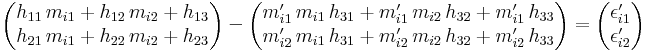
Each point-pair yields the following system of two linear equations \begin{pmatrix}h_{11}\,m_{i1}+h_{12}\,m_{i2}+h_{13}\\h_{21}\,m_{i1}+h_{22}\,m_{i2}+h_{23}\end{pmatrix}- \begin{pmatrix}m^\prime_{i1}\,m_{i1}\,h_{31}+m^\prime_{i1}\,m_{i2}\,h_{32}+m^\prime_{i1}\,h_{33}\\ m^\prime_{i2}\,m_{i1}\,h_{31}+m^\prime_{i2}\,m_{i2}\,h_{32}+m^\prime_{i2}\,h_{33}\end{pmatrix}= \begin{pmatrix}\epsilon^\prime_{i1}\\\epsilon^\prime_{i2}\end{pmatrix}

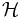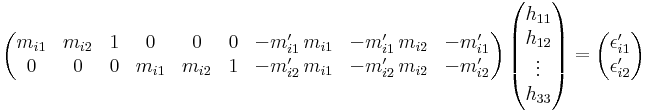
Isolating the elements of the unknown matrix \mathcal{H} gives \begin{pmatrix} m_{i1}&m_{i2}&1&0&0&0&-m^\prime_{i1}\,m_{i1}&-m^\prime_{i1}\,m_{i2}&-m^\prime_{i1}\\ 0&0&0&m_{i1}&m_{i2}&1&-m^\prime_{i2}\,m_{i1}&-m^\prime_{i2}\,m_{i2}&-m^\prime_{i2} \end{pmatrix}\, \begin{pmatrix}h_{11}\\h_{12}\\\vdots\\h_{33}\end{pmatrix}= \begin{pmatrix}\epsilon^\prime_{i1}\\\epsilon^\prime_{i2}\end{pmatrix}

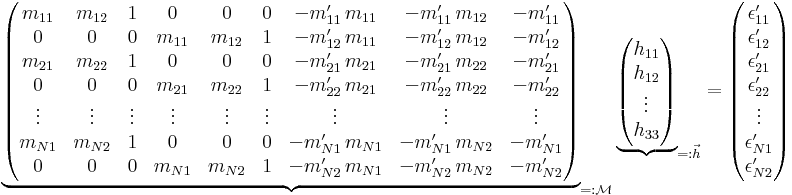
The combined system of all linear equations is \underbrace{\begin{pmatrix} m_{11}&m_{12}&1&0&0&0&-m^\prime_{11}\,m_{11}&-m^\prime_{11}\,m_{12}&-m^\prime_{11}\\ 0&0&0&m_{11}&m_{12}&1&-m^\prime_{12}\,m_{11}&-m^\prime_{12}\,m_{12}&-m^\prime_{12}\\ m_{21}&m_{22}&1&0&0&0&-m^\prime_{21}\,m_{21}&-m^\prime_{21}\,m_{22}&-m^\prime_{21}\\ 0&0&0&m_{21}&m_{22}&1&-m^\prime_{22}\,m_{21}&-m^\prime_{22}\,m_{22}&-m^\prime_{22}\\ \vdots&\vdots&\vdots&\vdots&\vdots&\vdots&\vdots&\vdots&\vdots\\ m_{N1}&m_{N2}&1&0&0&0&-m^\prime_{N1}\,m_{N1}&-m^\prime_{N1}\,m_{N2}&-m^\prime_{N1}\\ 0&0&0&m_{N1}&m_{N2}&1&-m^\prime_{N2}\,m_{N1}&-m^\prime_{N2}\,m_{N2}&-m^\prime_{N2} \end{pmatrix}}_{=:\mathcal{M}}\, \underbrace{\begin{pmatrix}h_{11}\\h_{12}\\\vdots\\h_{33}\end{pmatrix}}_{=:\vec{h}}= \begin{pmatrix}\epsilon^\prime_{11}\\\epsilon^\prime_{12}\\\epsilon^\prime_{21}\\\epsilon^\prime_{22}\\ \vdots\\\epsilon^\prime_{N1}\\\epsilon^\prime_{N2}\end{pmatrix}

To avoid the trivial solution 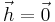\vec{h}=\vec{0} the constraint 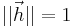||\vec{h}||=1 is introduced without loss of generality.

The calibration problem now has been reduced to the problem of finding 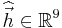\widehat{\vec{h}}\in\mathbb{R}^9 such that

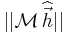  1. ||\mathcal{M}\,\widehat{\vec{h}}|| is minimal and
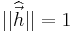
  2. ||\widehat{\vec{h}}||=1

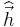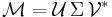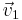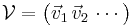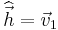\widehat{\vec{h}} can be computed using the Singular value decomposition (http://en.wikipedia.org/wiki/Singular_value_decomposition) \mathcal{M}=\mathcal{U}\,\Sigma\,\mathcal{V}^*, because these are the properties of the right handed singular vector \vec{v}_1 with the smallest singular value σ1 (where \mathcal{V}=\big(\vec{v}_1\,\vec{v}_2\,\cdots\big)). I.e. \widehat{\vec{h}}=\vec{v}_1.

Knowing the homography 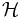\mathcal{H} already is sufficient for the Interactive Camera-Projector System.

[edit]

Intrinsic and extrinsic camera parameters

Please see references below ...

[edit]

See Also

[edit]

External Links

Bookmark and Share

Retrieved from "http://vision.eng.shu.ac.uk/mmvlwiki/index.php/Mimas_Camera_Calibration"
Personal tools